Selecting the proper spring forces for probes used to test printed circuit boards is not a casual consideration. The right spring force can make an important impact on contact reliability and will affect the cycle life of a probe. More importantly, determining the correct overall spring force is critical to ensuring the proper actuation of a test fixture and to preventing potential damage to the unit under test (UUT).
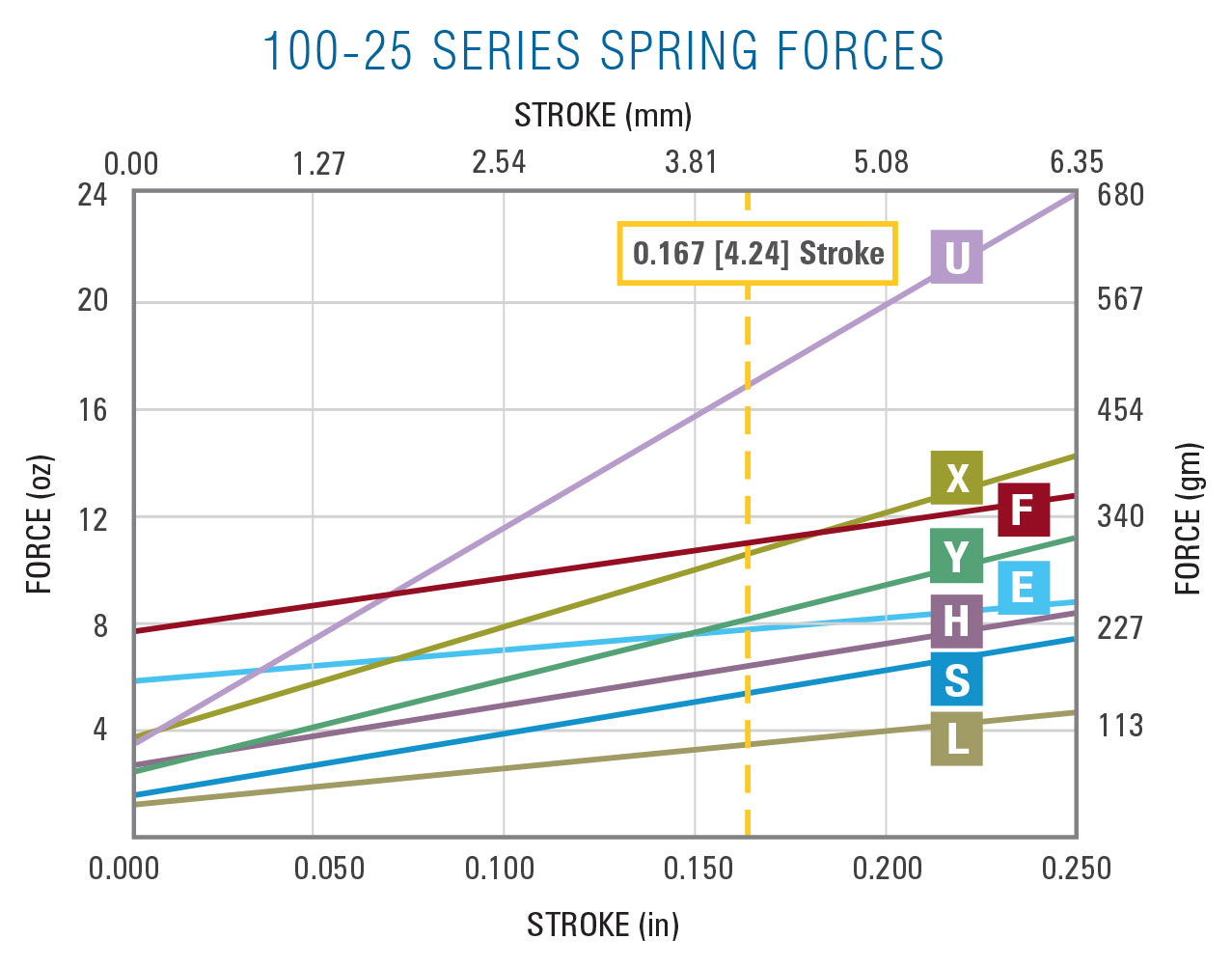
QA Technology’s springs are designed to be used at working stroke, typically 2/3 of the rated full stroke. This maximizes the cycle life of the probe without the risk of over stressing the spring.
QA’s high pre-load springs (E or F) offer a higher initial force through the full stroke to generate better probe tip penetration. The spring force is more consistent when the probe stroke is affected by variations due to board flex, fixture tolerances, and target heights.
Spring material is also an important factor when considering higher current applications. Stainless steel (SS) springs will typically carry higher amperage with increased temperature limits compared to music wire (MW) springs.
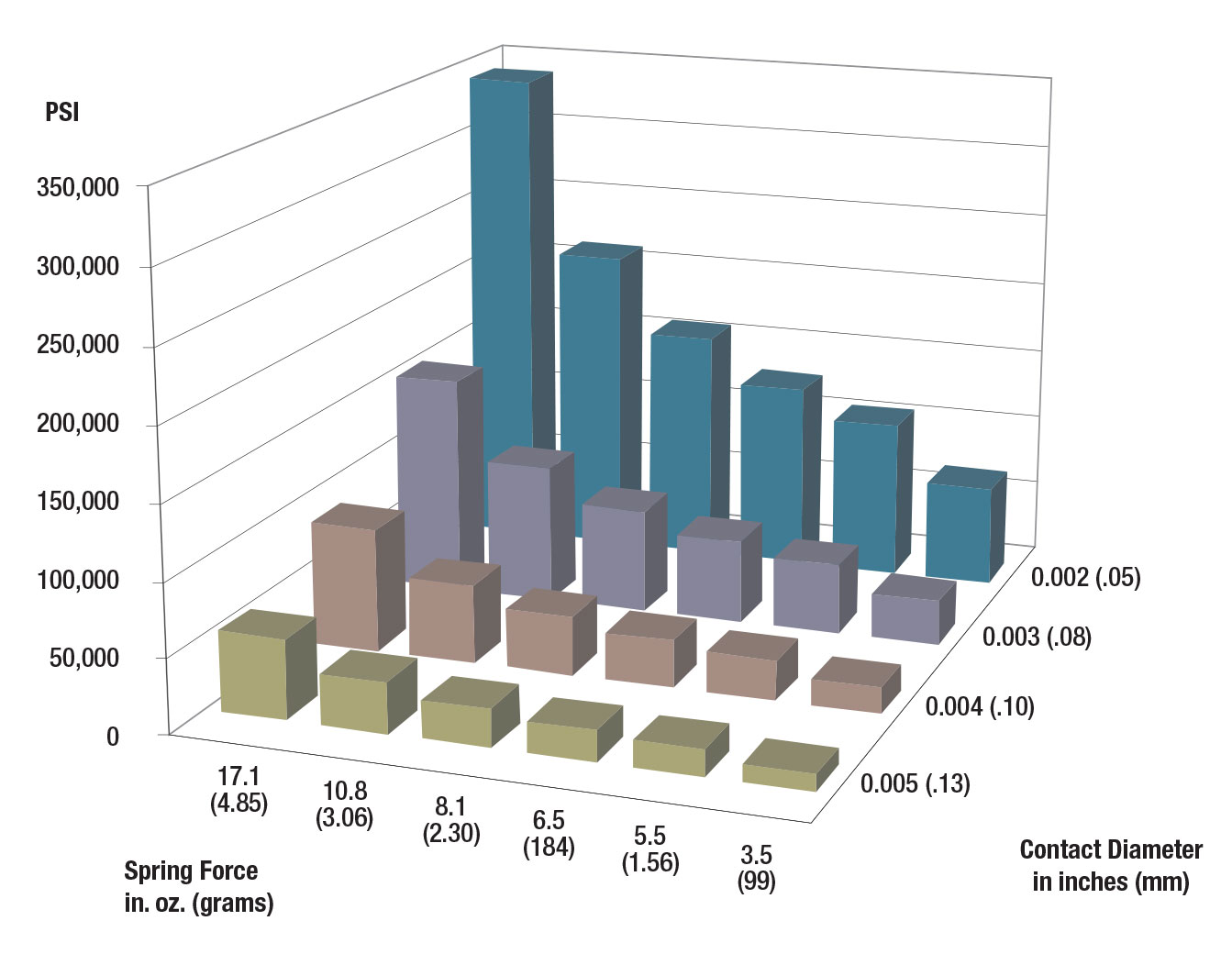
It is important to consider the condition of the UUT surfaces when selecting the proper spring force. When a probe makes contact, it causes deformation of the test target materials. The contact force for each probe must be high enough to penetrate any oxides, contaminants, or flux residues that can accumulate on both the test targets and the probe tips.
Sharp probe tips have the benefit of a reduced surface area which significantly increases the contact pressure applied. This allows the designer to select lower spring forces in a fixture and still achieve good contact.
By contrast, a probe tip which is flat or rounded by design will make contact over a larger area, causing less contact pressure. This may interfere with the probe’s ability to penetrate contamination layers. In these situations, a higher spring force may be necessary to achieve reliable electrical contact.
Probes are not always used at their rated working stroke. A probe’s spring force at any chosen stroke can be calculated with the formula:
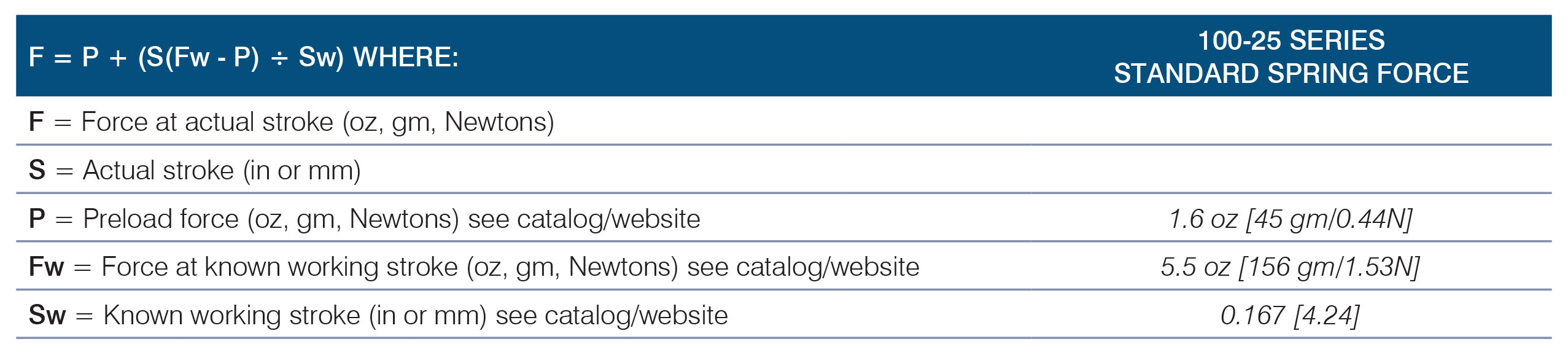
Example: Find the force at 0.200 [5.08] stroke for the standard force spring in the 100-25 series:
F = P + (S(Fw - P) ÷ Sw)
F = 1.6 + (0.200(5.5 - 1.6) ÷ 0.167) = 6.3 oz [179 gm/1.76N]
The collective force of the probes must not exceed the vacuum fixture system’s capability to move the tested product into contact with the probes. This formula can be used to calculate either the maximum number of probes of a given spring force, or the maximum spring force allowed for a given number of probes. An efficiency factor is added to account for fixture leaks, spring force tolerances, vacuum considerations (details below), etc. The spring force must never exceed the force applied by atmospheric pressure.
Example: 6" x 10" [15.2 cm x 25.4 cm] board and 5.5 oz [156 gm] probes.
By using the total area of the UUT in the formula, the approximate maximum number of probes in a fixture can be calculated:

Avoid densely concentrated areas of high force so as not to damage the product or cause fixture actuation problems.
Concentrations of probes around connectors or large pin packages may exceed one (1) atmosphere in a small area of the product as long as the total force is below the maximum limit. Uneven probe distribution can cause excessive flexing of the product and may affect the vacuum seal – particularly with thin boards.

When calculating spring force limitations, the efficiency factor is used to define the vacuum system’s ability to overcome the total probe spring force. The two factors that are typically referenced are air flow in cubic feet per minute (CFM) and amount of vacuum in inches of mercury. Cubic feet per minute is the measure of the vacuum system’s ability to move a volume of air over time. The higher the CFM, the better the vacuum system’s ability to draw the product down quickly and overcome initial seal leakage. A vacuum reservoir will compensate for low pump CFM, absorbing the initial rush as the vacuum system evacuates the fixture and seats the product. Inches of mercury is the measure of the system’s ability to draw a complete vacuum. Thirty inches of mercury is one atmosphere (a full vacuum). Anything less than 30 inches can be considered a percentage of one (1) atmosphere and used in the probe limit calculation above as the efficiency factor. The example used in the limit calculation was 0.60 which represents 18 inches of mercury in a high elevation facility divided by 30 inches.
Check spring force selection or changes with the fixture manufacturer since these choices are closely tied to the fixture design.
Contact pressure (a function of spring force and tip geometry) must be high enough to penetrate oxides and contaminants that accumulate on both the test targets and the probe tips.
Electrical performance depends largely on the combination of tip sharpness and geometry, as well as on the spring force of a probe. While increasing spring force applies more contact pressure to the test targets, be cautious because it also adds to the overall forces applied to the UUT.